In this blog, let us understand the linear equation definition.

Linear equation definition

A�linear equation�is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation.

Types of Equation

There are two types of equations, first is arithmetic equations and 2^nd is algebraic equations.

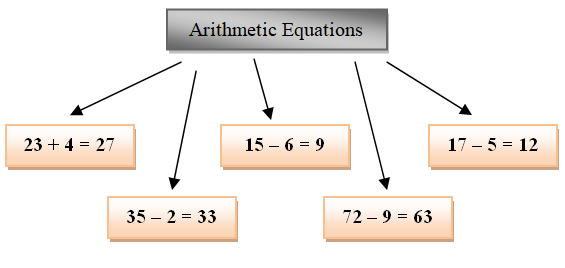
23 + 4 = 27,
15 � 6 = 9,
17 � 5 = 12,
35 � 2 = 33 and
72 � 9 = 63

These equations are arithmetic equations.

Now, look at these equations. Such equations having variables are called algebraic equations. 

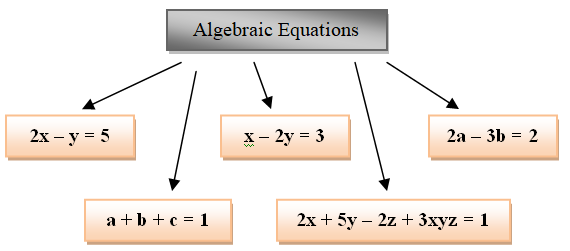
This is an equation.

6 x � 5 = 19

Let us learn the various components of this equation. Here x is the variable, 6 is the coefficient of x and the sign of �equal� is to divide it into 2 sides i.e., the left-hand side & right-hand side. In LHS we have 6x � 5 and in RHS we have 19, a constant.

This equation belongs to the family of linear equations. A linear equation is an equation that has only one variable with degree 1.

How to solve this equation?

6x � 5 + 5 = 19 + 5
6x = 24
6x/6 = 24/6
x = 4

To solve we have to put the value of x such that LHS becomes equal to RHS. For this first, we will add 5 on both sides. We are left with 6x is equal to 24. Dividing both sides with 6, we have x is equal to 4. So x is equal to 4 is the required solution.

Let's discuss reduction in linear form and simple form. First, we will begin with a reduction in a simple form. Consider this example.

Example: 6x + 1/3+ 1 = x -3 /6

Multiplying both sides by 6

6(6x + 1)/ 3+ 1 x 6 = 6(x -3)/6

=2 (6x + 1) + 6 = x � 3

=12x + 2 + 6 = x � 3

=12x + 8 = x � 3

Taking like�terms on one side

=12x � x  = � 3- 8

=11x  = � 11

=x = � 1

Let us check our solution. For this we need to put the value of x i.e. -1 in place of x. we will consider LHS first.

LHS = (6x + 1)/ 3+ 1

=6(-1)+1/3+1

= -5 /3+ 1

Taking LCM we have

= -5+3/3

=-2/3

RHS= x -3 /6

= (-1) � 3/6

= -4/6

= -2/3

Therefore LHS = RHS

Now we will discuss the equations reducible to linear form. Let us consider this example. Solve x + 1/ 2x+ 3 = 3 by 8

Solution: x + 1/ 2x+ 3 = 3 by 8

x + 1/ 2x+ 3 (2x + 3) = 3 / 8 (2x + 3)

(x + 1) = 3(2x + 3)/ 8.

Multiplying both sides by 8

=8 (x + 1) = 3 (2x + 3)

8x + 8 = 6x + 9

8x -6x = 9 � 8

2x =1

x =1/2

Check: Numerator of LHS = � + 1= 3/2

Denominator of LHS = 2x + 3 = 2 x 1by 2 + 3 = 1 + 3 = 4

LHS = numerator � denominator

= 3/2 � 4 =3/2 x � = 3/8

LHS = RHS.

Read More:
Application Of Linear Equation in Maths With Examples: Maths Class 8